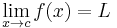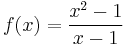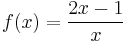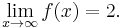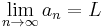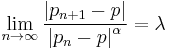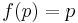Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value.[1] The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric space.[2] Limits are essential to calculus (and mathematical analysis in general) and are used to define continuity, derivatives, and integrals.
The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory.
In formulas, limit is usually abbreviated as lim as in lim(an) = a, and the fact of approaching a limit is represented by the right arrow (→) as in an → a.
Contents |
Limit of a function
Suppose f(x) is a real-valued function and c is a real number. The expression
means that f(x) can be made to be as close to L as desired by making x sufficiently close to c. In that case, the above equation can be read as "the limit of f of x, as x approaches c, is L".
Augustin-Louis Cauchy in 1821,[3] followed by Karl Weierstrass, formalized the definition of the limit of a function as the above definition, which became known as the (ε, δ)-definition of limit in the 19th century. The definition uses ε (the lowercase Greek letter epsilon) to represent a small positive number, so that "f(x) becomes arbitrarily close to L" means that f(x) eventually lies in the interval (L - ε, L + ε), which can also be written using the absolute value sign as |f(x) - L| < ε.[3] The phrase "as x approaches c" then indicates that we refer to values of x whose distance from c is less than some positive number δ (the lower case Greek letter delta)—that is, values of x within either (c - δ, c) or (c, c + δ), which can be expressed with 0 < |x - c| < δ. The first inequality means that the distance between x and c is greater than 0 and that x ≠ c, while the second indicates that x is within distance δ of c.[3]
Note that the above definition of a limit is true even if f(c) ≠ L. Indeed, the function f(x) need not even be defined at c.
For example, if
then f(1) is not defined (see division by zero), yet as x moved arbitrarily close to 1, f(x) correspondingly approaches 2:
| f(0.9) | f(0.99) | f(0.999) | f(1.0) | f(1.001) | f(1.01) | f(1.1) |
| 1.900 | 1.990 | 1.999 | ⇒ undef ⇐ | 2.001 | 2.010 | 2.100 |
Thus, f(x) can be made arbitrarily close to the limit of 2 just by making x sufficiently close to 1.
In addition to limits at finite values, functions can also have limits at infinity. For example, consider
- f(100) = 1.9900
- f(1000) = 1.9990
- f(10000) = 1.99990
As x becomes extremely large, the value of f(x) approaches 2, and the value of f(x) can be made as close to 2 as one could wish just by picking x sufficiently large. In this case, the limit of f(x) as x approaches infinity is 2. In mathematical notation,
Limit of a sequence
Consider the following sequence: 1.79, 1.799, 1.7999,... It can be observed that the numbers are "approaching" 1.8, the limit of the sequence.
Formally, suppose a1, a2, ... is a sequence of real numbers. It can be stated that the real number L is the limit of this sequence, namely:
to mean
- For every real number ε > 0, there exists a natural number n0 such that for all n > n0, |an − L| < ε.
Intuitively, this means that eventually all elements of the sequence get arbitrarily close to the limit, since the absolute value |an − L| is the distance between an and L. Not every sequence has a limit; if it does, it is called convergent, and if it does not, it is divergent. One can show that a convergent sequence has only one limit.
The limit of a sequence and the limit of a function are closely related. On one hand, the limit as n goes to infinity of a sequence a(n) is simply the limit at infinity of a function defined on the natural numbers n. On the other hand, a limit L of a function f(x) as x goes to infinity, if it exists, is the same as the limit of any arbitrary sequence an that approaches L, and where an is never equal to L. Note that one such sequence would be L + 1/n.
Convergence and fixed point
A formal definition of convergence can be stated as follows. Suppose 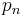 as
as  goes from
goes from 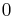 to
to 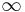 is a sequence that converges to a fixed point
is a sequence that converges to a fixed point  , with
, with 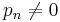 for all
for all  . If positive constants
. If positive constants  and
and  exist with
exist with
then 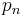 as
as  goes from
goes from 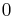 to
to 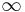 converges to
converges to  of order
of order  , with asymptotic error constant
, with asymptotic error constant 
Given a function 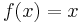 with a fixed point
with a fixed point  , there is a nice checklist for checking the convergence of p.
, there is a nice checklist for checking the convergence of p.
- 1) First check that p is indeed a fixed point:
- 2) Check for linear convergence. Start by finding
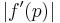 . If....
. If....
 |
then there is linear convergence |
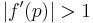 |
series diverges |
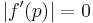 |
then there is at least linear convergence and maybe something better, the expression should be checked for quadratic convergence |
- 3) If it is found that there is something better than linear the expression should be checked for quadratic convergence. Start by finding
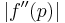 If....
If....
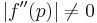 |
then there is quadratic convergence provided that 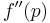 is continuous is continuous |
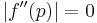 |
then there is something even better than quadratic convergence |
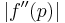 does not exist does not exist |
then there is convergence that is better than linear but still not quadratic |
Topological net
All of the above notions of limit can be unified and generalized to arbitrary topological spaces by introducing topological nets and defining their limits.
An alternative is the concept of limit for filters on topological spaces.
See also
- Limit of a sequence
- Rate of convergence: the rate at which a convergent sequence approaches its limit
- Limit of a function
- One-sided limit: either of the two limits of functions of a real variable x, as x approaches a point from above or below
- List of limits: list of limits for common functions
- Squeeze theorem: finds a limit of a function via comparison with two other functions
- Limit in category theory
- Asymptotic analysis: a method of describing limiting behavior
- Big O notation: used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity
Notes
- ^ Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN 0-495-01166-5.
- ^ Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill. ISBN 0-07-054235-X.
- ^ a b c Larson, Ron; Edwards, Bruce H. (2010). Calculus of a single variable (Ninth ed.). Brooks/Cole, Cengage Learning. ISBN 9780547209982.
- ^ Numerical Analysis, 8th Edition, Burden and Faires, Section 2.4 Error Analysis for Iterative Methods
External links
- Weisstein, Eric W., "Limit" from MathWorld.
- Mathwords: Limit